这篇文章总结了几种定价美式期权的方法并且提供了相应的模板。欧式期权普遍交易于商品市场。它具有闭合定价公式,该公式由传统的Black-Scholes模型推导得出,该公式在电子表格程序和编程语言中很容易得以实现。但在交易所交易得最多的是美式期权。美式期权可以在到期日之前行权,这带来更多灵活性的同时也给发行期权方带来了更多风险,这也意味着美式期权比欧式期权有更高的价格。
美式期权没有闭合解,但是它有不少数值方法和近似解,下面就介绍了一些最常用的方法。以及在QuantPlus Analytic中利用相应方法计算得出的结果。
Barone-Adesi & Whaley近似法
这个方法将美式期权的价值分成两个部分,第一部分是欧式期权的价值,第二部分是提前行权的价值。第二部分可以通过偏微分方程来解得,Barone-Adesi & Whaley用了一个二项式来估算,因此这个方法又被称为二项式方法(Quadratic Method)。
这个估算的模型可以被用于付连续红利、常红利、离散红利的期权。
详细的内容可参见: “Efficient analytic approximation of american option values”, Journal of Finance 42, 301-320. C code for the Barone-Adesi & Whaley approximation。点击链接可见 。
二叉树模型法
二叉树模型模拟出股票价格在一段时间内的价格,这就让它们非常适合定价允许提前行权的美式期权。
二叉树(三叉树)计算方法包含以下步骤:
1. 建立一个股票价格的二叉树模型。在树的每一个节点,价格可以上涨或下跌;
2. 计算期权在到期日的价格。
3. 期权在到期日之前的任意价格可以通过回溯的方法计算。
Cox-Ross-Rubinstein 模型
Cox, Ross and Rubinstein二叉树 有如下公式
![]()
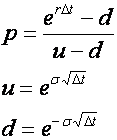
这里p、u、d的唯一解确保了在短时间间隔内二叉树模型能匹配无风险世界中资产的均值和波动率,此外这也确保了在多步骤的模型中标的资产的价格是关于其起始价格 S0对称的。
多步二叉树模型
下面用示例描述了两步的二叉树模型资产演化模型:

由上图可得知资产在下一个时间段有向上的价格 Su 或者向下的价格 Sd。第二个时间段, 资产价格 Su 可能会有两个价格 Suu 或者 Sud。第一个时间段向下的价格 Sd 会有价格 Sdu 或者 Sdd。如果 Sud=Sdu 该资产价格会再重合。
由以上CRR公式可以产生一个再重合的树形结构,该结构在多个时间段的情况下就会产生如下的树形结构,会围绕价格S0上下波动。
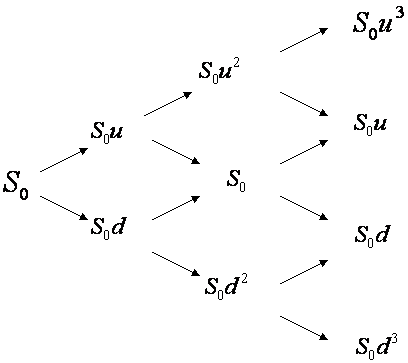
从今天开始到到期日,时间段被分成很小的时间步。未来资产的演化树结构可以被计算显示出来。每个树形结构的每个点称为一个节点。该树形结构每个节点就是从今天开始到未来任意时刻资产的价格演化。
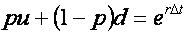
计算到期时的回报
计算期权价格的第二步是计算在到期日每一个节点的回报,这对应着在二叉树最右端所有的节点。
总体来说计算回报是基于很多不同的因素的,比如计算call和put期权可以用以下标准公式:
| 类型 | 支付 |
| Put | VN = max(X-SN,0) |
| Call | VN = max(SN-X,0) |
其中
- N 表示到期时的节点
- VN 是期权价格
- X i是行权价格
- SN 是标的物价格
贴现回报
定价期权的第三步是用二项模型将期权在到期日的回报贴现到今天。这个可以通过向后归纳完成,由后往前在各个网格通过按顺序计算。具体可参照一下公式:
| 类型 | 反推函数 |
| 欧式Put或者Call | Vn = e-rΔt(pVu+(1-p)Vd) |
| 美式Put | Vn = max(X-Sn,e-rΔt(pVu+(1-p)Vd)) |
| 美式Call | Vn = max(Sn-X,e-rΔt(pVu+(1-p)Vd)) |
其中:
- n表示到期前的第n个时间节点
- Vn 是期权价格
- X 是行权价格
- Sn 是标的资产价格
- p 是资产价格上涨概率
- Vu是在时间点 n+1的向上节点的期权价格
- Vd是在时间点 n+1的向上节点的期权价格
- r 是无风险利率
- Δt 是模型每个节点的时间步长
注意此处的n是从到期时间N到今天的时间0.
二叉树优点如下:
- · 易于理解,不需要复杂的数学公式
- · 可在电子表格中迅速建模
- · 可包含红利
但是二叉树不能得出完全准确的期权价值(因为它们是离散的),而且它们还假设了常波动率。
